Skip to main content

Of Solenoids and Spherical Electromagnets

Working on modelling the magnetic field that will be used to quench a 4 inch lead superconducting sphere in the h-ray experiment.  The first trial was just to place the superconductor in a surrounding solenoid electromagnet.  The correct magnitude of field can be obtained that way, but the uniformity isn't great.  Adding more layers of windings increases the field strength but doesn't help with the uniformity.  Each level of coils basically linearly increases the field strength.  The percent change in field with length along the solenoid, (shown on the x axis below), stays pretty much the same though.  The graphs shown are for one, two, and three layers of coils.


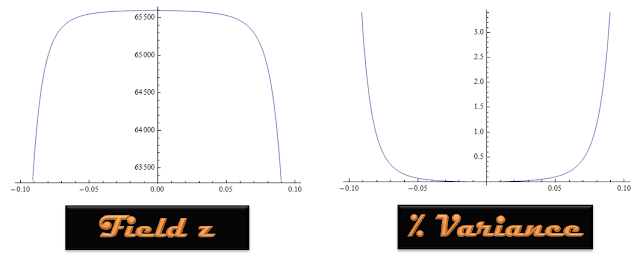
While looking around for a coil design that would give a more uniform field I came across a patent[1] that described a spherically wound electromagnet and promised a uniform field within the sphere.  I tried modified the model to handle a spherically wound coil and got the results along the up-down axis, (z), and the equatorial axis, (r), of the coil shown in the graphs below.  The z direction has a very nice improvement.  The radial direction, even with it's 17% or so variance between the field at the center and the edge of the coil is still far better than the plain-old solenoid designs.



Labels:

Comments

  1. John ShearingMarch 25, 2016 at 5:43 AM

    Have you looked at this type of spherical electromagnet for your experiment.

    This is the picture of it:
    http://www.justodians.org/SphericalMagnet/01ElecMagPic1.htm

    This is the patent application which is now in the public domain and free for all to use:
    http://www.justodians.org/SphericalMagnet/PatentApp.htm

    I invented it years ago but never had the opportunity to experiment with it.

    Good Luck
    John

    ReplyDelete

Post a Comment

Please leave your comments on this topic:

Popular posts from this blog

The Valentine's Day Magnetic Monopole

There's an assymetry to the form of the two Maxwell's equations shown in picture 1.  While the divergence of the electric field is proportional to the electric charge density at a given point, the divergence of the magnetic field is equal to zero.  This is typically explained in the following way.  While we know that electrons, the fundamental electric charge carriers exist, evidence seems to indicate that magnetic monopoles, the particles that would carry magnetic 'charge', either don't exist, or, the energies required to create them are so high that they are exceedingly rare.  That doesn't stop us from looking for them though! Keeping with the theme of Fairbank[1] and his academic progeny over the semester break, today's post is about the discovery of a magnetic monopole candidate event by one of the Fairbank's graduate students, Blas Cabrera[2].  Cabrera was utilizing a loop type of magnetic monopole detector.  Its operation is in...
1 comment
Read more

Cool Math Tricks: Deriving the Divergence, (Del or Nabla) into New (Cylindrical) Coordinate Systems

Now available as a Kindle ebook for 99 cents ! Get a spiffy ebook, and fund more physics The following is a pretty lengthy procedure, but converting the divergence, (nabla, del) operator between coordinate systems comes up pretty often. While there are tables for converting between common coordinate systems , there seem to be fewer explanations of the procedure for deriving the conversion, so here goes! What do we actually want? To convert the Cartesian nabla to the nabla for another coordinate system, say… cylindrical coordinates. What we’ll need: 1. The Cartesian Nabla: 2. A set of equations relating the Cartesian coordinates to cylindrical coordinates: 3. A set of equations relating the Cartesian basis vectors to the basis vectors of the new coordinate system: How to do it: Use the chain rule for differentiation to convert the derivatives with respect to the Cartesian variables to derivatives with respect to the cylindrical variables. The chain ...
11 comments
Read more

More Cowbell! Record Production using Google Forms and Charts

First, the what : This article shows how to embed a new Google Form into any web page. To demonstrate ths, a chart and form that allow blog readers to control the recording levels of each instrument in Blue Oyster Cult's "(Don't Fear) The Reaper" is used. HTML code from the Google version of the form included on this page is shown and the parts that need to be modified are highlighted. Next, the why : Google recently released an e-mail form feature that allows users of Google Documents to create an e-mail a form that automatically places each user's input into an associated spreadsheet. As it turns out, with a little bit of work, the forms that are created by Google Docs can be embedded into any web page. Now, The Goods: Click on the instrument you want turned up, click the submit button and then refresh the page. Through the magic of Google Forms as soon as you click on submit and refresh this web page, the data chart will update immediately. Turn up the:...
Post a Comment
Read more