Radiation angle of the Project TouCans dipole part II

Let's get going. Here's the figure explaining the formula we'll be using. It's the one I alluded to yesterday. The formula of which I speak will tell us the minimum F2 height required for a radio signal to skip off the ionoshphere and back to another station. The geometry used to derive the formula has a single constraint: the lowest angle, (radiation angle), the radio signal is allowed to leave the transmitting antenna at is 0 degrees—in otherwords, parallel with and tangential to the ground.

The formula will be used in a larger application to programmatically determine the number of skips that are required to make a QSO via the F2 layer of the ionosphere. I'll explain more in a bit.

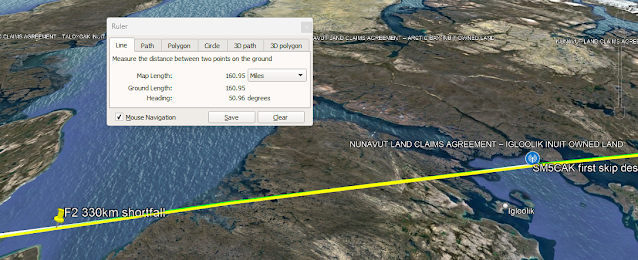
Picking up where we left off yesterday, we're using the measured height of the ionosphere in Pt. Arguello ~330km, and we're assuming the signal skipped twice, (remember that in yesterday's post we saw that if the signal only skipeed once, the only way to reach Sweden was in fact to go unerground.) The path of propagation with these assumptions didn't quite make it the half-way distance to Sweden. Instead, it went underground about here,

about 161 miles short of it's goal. Remember that goal was to make it half the distance to the station in Sweden where the second skip would bring the signal the rest of the way in.

To further elucidate, that landing site is where the peak of the original F2 skip was when we were looking at a single skip. In other words, we know exactly, (mathematically), where the landing site fo the first skip should be for the purposes of this problem.

A final reminder from yesterday: the skip was only 160 miles short on a 5000 mile path, so that's actually really, really close, and for a diffracting radio wave, close enough.

So, that's the results we saw with the measured F2 height of 330 km at Pt. Arguello, CA. But, what would the exact height need to be, (calculated using the formula derived above)? The formula derived above shows that the minimum F2 height to make the double skip we discussed is 381.2190729008156 km. Plugging that into the kml map gives us a path that does in fact land at the half way point. Wooo! Math, and specifically, this derviation works!

Here's a view from Google Earth Pro where we can see the new path sailing in over the landing point of the 330 km F2 path.

Here's a gif of the surrounding region

Finally, here's a video showing that the signal lands right at the midpoint of the path to Sweden:

Another thing that makes me grin about all this, is that you can see the sun is just over the horizon along this portion of the path ala grey line!

The formula above involves the angle that's swept out along the surface of the Earth between stations. How do we get that angle? It turns out we use cross products again. Here are the steps
1. Convert both locations to Cartesian coordinats

2. Complete the cross product

3. Take the magnitude of the cross product

4. Take the arcsin of that magnitude. The result is the angle swept out along the sphere between the two stations.

I'm trying to keep the notes here short with only the highlights—mostly so I'll keep writing—so, rather than lay out all the math details here, let me point you to the Sage enabled cocalc worksheet for this series of posts.

And that's all for today! Since two skips involved the signal leaving our dipole at 0 degrees, and then missing by 160 miles or so, tomorrow, we're going to try three skips. Watch here for more.

The steps so far:

Get Pt. Arguello F2 height, assume that's the height along entire path

Map skip path

It goes under the Earth

Assume there are two skips

Use the same F2 height, and map a path to the midway pont on the QSO path

It goes under the Earth 160 miles short of the midway point

Calculate the minimum F2 height to make that skip

The minimum F2 height is 381.2 km rather than 330 km

Map the skip to the endpoint using that height

The skip lands exactly at the midpoint verifying that the forumula for F2_min works

Next Steps:

Next step: talk about the Idaho and Thule ionosondes

Next step: Talk about the RBN stations in Canada and the three skip scenario. Look at their SNR number. It looks like the first of the three skips will land pretty close the Canada RBN stations.

Next step: Map three skips

The Valentine's Day Magnetic Monopole

There's an assymetry to the form of the two Maxwell's equations shown in picture 1. While the divergence of the electric field is proportional to the electric charge density at a given point, the divergence of the magnetic field is equal to zero. This is typically explained in the following way. While we know that electrons, the fundamental electric charge carriers exist, evidence seems to indicate that magnetic monopoles, the particles that would carry magnetic 'charge', either don't exist, or, the energies required to create them are so high that they are exceedingly rare. That doesn't stop us from looking for them though! Keeping with the theme of Fairbank[1] and his academic progeny over the semester break, today's post is about the discovery of a magnetic monopole candidate event by one of the Fairbank's graduate students, Blas Cabrera[2]. Cabrera was utilizing a loop type of magnetic monopole detector. Its operation is in...

Cool Math Tricks: Deriving the Divergence, (Del or Nabla) into New (Cylindrical) Coordinate Systems

Now available as a Kindle ebook for 99 cents ! Get a spiffy ebook, and fund more physics The following is a pretty lengthy procedure, but converting the divergence, (nabla, del) operator between coordinate systems comes up pretty often. While there are tables for converting between common coordinate systems , there seem to be fewer explanations of the procedure for deriving the conversion, so here goes! What do we actually want? To convert the Cartesian nabla to the nabla for another coordinate system, say… cylindrical coordinates. What we’ll need: 1. The Cartesian Nabla: 2. A set of equations relating the Cartesian coordinates to cylindrical coordinates: 3. A set of equations relating the Cartesian basis vectors to the basis vectors of the new coordinate system: How to do it: Use the chain rule for differentiation to convert the derivatives with respect to the Cartesian variables to derivatives with respect to the cylindrical variables. The chain ...

More Cowbell! Record Production using Google Forms and Charts

First, the what : This article shows how to embed a new Google Form into any web page. To demonstrate ths, a chart and form that allow blog readers to control the recording levels of each instrument in Blue Oyster Cult's "(Don't Fear) The Reaper" is used. HTML code from the Google version of the form included on this page is shown and the parts that need to be modified are highlighted. Next, the why : Google recently released an e-mail form feature that allows users of Google Documents to create an e-mail a form that automatically places each user's input into an associated spreadsheet. As it turns out, with a little bit of work, the forms that are created by Google Docs can be embedded into any web page. Now, The Goods: Click on the instrument you want turned up, click the submit button and then refresh the page. Through the magic of Google Forms as soon as you click on submit and refresh this web page, the data chart will update immediately. Turn up the:...

Copasetic Flow

Search This Blog