Robert W. Crown Memorial State Beach POTA

There's a beach on the Bay just south of Oakland in Alameda. I wouldn't have known if not for ham radio and parks on the air POTA.

Headed to the beach. The San Francisco skyline

Park:

Robert W. Crown Memorial State Beach K-3550.

Getting there

I took the Alameda Seaplane Ferry! It's a really nice ride with plenty of things to look at like the San Francisco Skyline above, the Bay Bridge, and the USS Hornet, (after the transit map below.)

Other Things To See On The Way

USS Hornet

The museum ship, the USS Hornet, is a short walk from the ferry terminal. I didn't get to stop in the day of the POTA, but I'd like to soon.

Furniture

If you're in need of a couch, the Pottery Barn clearance store is on the walk from the ferry terminal to the beach. Sooo many discounted white couches.

Lake Chalet

I met part of my extended family in Oakland for dinner. Making the bus connection was a little intense thanks to my planning skills, but I was able to catch the 20 about a mile from the beach. I rode to downtown Oakland where I walked to the Lake Chalet on Lake Merritt. The food is delicious, the staff is friendly, and the restaurant's situated in a gorgeous park near a lake.

Radio Details:

The Rockmite was suspended in the antenna per normal these days. There seems to have been a loose connection to the BNC connector that was causing some issues, hence the low signal reports below I assume.

QSO/RBN spot map:

Interactive:

Happenings of Interest

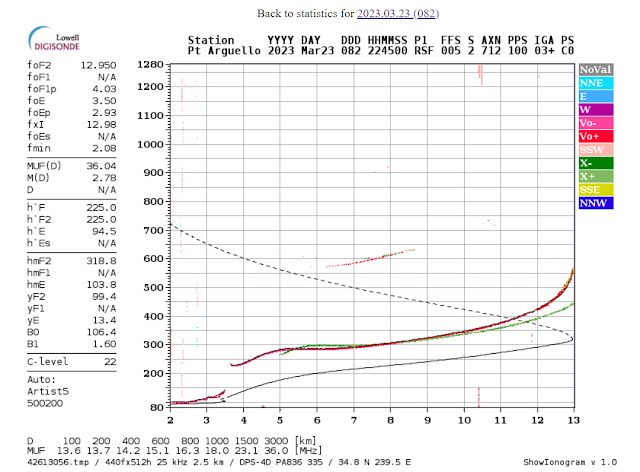
Frankly, the weather was just nice, and that's a relief and a surprise after the last few weeks. There were a few crows building a nest, a few squirrels gamboling around, and a few hikers were out wandering up and down the beach trail.

Also, the radio reached North Carolina! Looking back on the ionogram at that time, the F2 layer was higher than it has usually been

QSO Log

Callsign	rx RST	tx RST	Time (GMT)	Frequency
WA6GFE	599	539	21:20	14057.6
W0AZ	449	599	21:26	14057.6
NZ7Q	559	559	22:35	14057.6
N4EX	229	339	22:42	14057.6
NT6E	529	599	23:02	14057.6
WB7DND	549	549	23:30	14057.6
KJ7DT	559	559	22:47	14057.6
NA6JD	529	599	00:12	14057.6
N6KM	229	599	23:57	14057.6
AG7S	559	599	23:59	14057.6
AI7BM	539	599	00:03	14057.6

POTA tx QSL:

QSL rx album:

References

POTA (Parks on the Air)

Comments

Cool Math Tricks: Deriving the Divergence, (Del or Nabla) into New (Cylindrical) Coordinate Systems

Now available as a Kindle ebook for 99 cents ! Get a spiffy ebook, and fund more physics The following is a pretty lengthy procedure, but converting the divergence, (nabla, del) operator between coordinate systems comes up pretty often. While there are tables for converting between common coordinate systems , there seem to be fewer explanations of the procedure for deriving the conversion, so here goes! What do we actually want? To convert the Cartesian nabla to the nabla for another coordinate system, say… cylindrical coordinates. What we’ll need: 1. The Cartesian Nabla: 2. A set of equations relating the Cartesian coordinates to cylindrical coordinates: 3. A set of equations relating the Cartesian basis vectors to the basis vectors of the new coordinate system: How to do it: Use the chain rule for differentiation to convert the derivatives with respect to the Cartesian variables to derivatives with respect to the cylindrical variables. The chain ...

The Alcubierre Warp Drive Tophat Function and Open Science with Sage

I transferred yesterday's Mathematica file with the Alcubierre warp drive[2] line element and space curvature calculations to the +Sage Mathematical Software System today, (the files been added to the public repository [3]). If you haven't used Sage before, it's a Python based software package that's similar in functionality to Mathematica. Oh, and it' free. I also worked a little more on understanding the theory, but frankly, I made far more progress with the software than the theory. What follows will be a little more of the Alcubierre theory, plus, a cool Sage interactive demo of one of the Alcubierre functions[1], as well as a bit about my first experience with using Sage. Theory The theory is fun, but it's moving slowly. Here's the chalk board from this morning's discussion Alcubierre setup the derivation using something called the 3+1 formalism which means we consider space to be flat, (in this case), slices that are labelled ...

The Valentine's Day Magnetic Monopole

There's an assymetry to the form of the two Maxwell's equations shown in picture 1. While the divergence of the electric field is proportional to the electric charge density at a given point, the divergence of the magnetic field is equal to zero. This is typically explained in the following way. While we know that electrons, the fundamental electric charge carriers exist, evidence seems to indicate that magnetic monopoles, the particles that would carry magnetic 'charge', either don't exist, or, the energies required to create them are so high that they are exceedingly rare. That doesn't stop us from looking for them though! Keeping with the theme of Fairbank[1] and his academic progeny over the semester break, today's post is about the discovery of a magnetic monopole candidate event by one of the Fairbank's graduate students, Blas Cabrera[2]. Cabrera was utilizing a loop type of magnetic monopole detector. Its operation is in...

Copasetic Flow

Search This Blog