Simulations! Everywhere Simulations! Lab Book 2014_07_31

Summary:
Excuse a brief moment of frivolity please.  OMG, This is So *#($&#@ cool!!!

OK, now that I've got that out of my system we can move on.  The can crusher simulator port from IDL to Sage is complete and it's working spectacularly well!  I was able to run simulations to find out what the temperature of the can would increase to due to the magnetic pulse.  I was also able to plot the magnetic field in a sphere around the pulisng coil to determine if the coil as specified would provide a high enough magnetic field to quench the entire superconducting Pb sample at once.  Meanwhile, work is continuing on fixing the vacuum leak detector.  I was unable to find an instrument panel bulb to attempt the kluge fix suggested below, so it looks like I'll be ordering a replacement part instead.

If you're new to the experiment, you can find background by scrolling to the bottom of the page.

Lab Book 2014_07_30     Hamilton Carter

Vacuum Leak Detector Work

Still looking into a replacement for the Pirani gauge.  We don’t have any bulbs here that will substitute for the 70 ohms specified here.

Proposed procedure for calibrating bulb

1.       Use potentiometer and voltmeter to determine at what resistance the leak detector will turn on the diffusion pump.  The potentiometer will be inserted between the pins of the PI-1 and adjusted till the diffusion pump power comes on.  This will be the resistance the detector wants to see to turn on the diffusion pump.  The voltmeter will watch the disconnected power line to the diffusion pump to determine when power is applied to the pump.

2.       Place the proposed bulb in vacuum.  Run the same current through it and measure its resistance vs. pressure, with a bridge?  Check the pressure in the chamber with a calibrated vacuum meter.  Check for the resistance to reach the proper value at the proper pressure so that the diffusion pump will not be damaged.

3.       if the resistance is not correct at the correct pressure, try making a resistive combination to bring the resistance into range.

Can Crusher Simulation

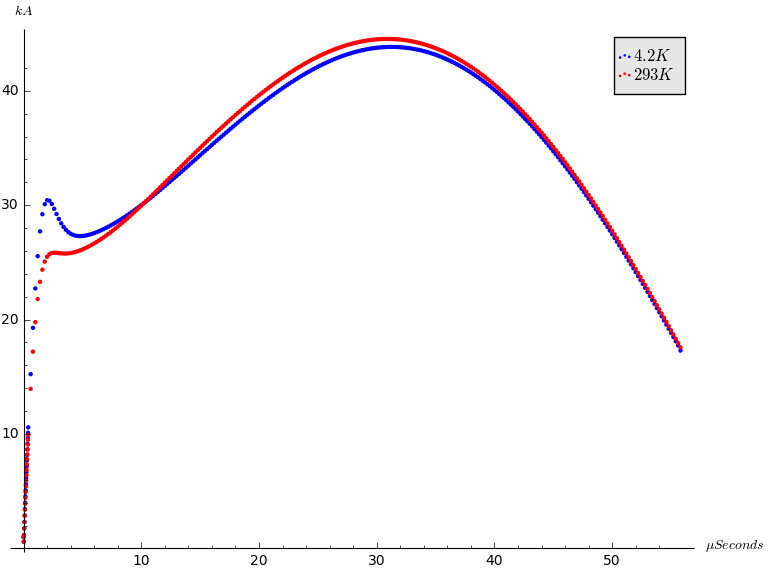
I started to ask interesting questions using the simulator today.  Here’s a graph comparing the driving current at room temperature and at the temperature of our sample, 4.2 degrees Kelvin.

Notice the initial spike in current on the lower temperature curve.  I’m wondering if this can be made to help quench the superconductor even more quickly.

The heat created by the can crushing currents should be able to be related to temperature using the heat capacity of the material.  Actually, the code that converts to temperature is already in the simulation.  I just need to store the values per time tick.  DONE!

Here’s the graph of the temperature change in the can with the can starting at 293 K vs. 4.2 K.  This should be further updated to include the entire volume of liquid helium in the Dewar.  At the moment, the calculation only takes into account the mass of the can.  It can be seen that in the coarse sense, there is not much difference after 20 microseconds or so.

The initial results for the magnetic field along the surface of the superconductor look troublesome.  More soon.

However, before we get into that, here are the current curves for the planned largest and smallest Pb spherical sample sizes at room temperature.

A simulation is being run at liquid helium temperatures.  The next step is to put in the material constant values for Pb and modify the moving coils so they fit on a spherical form matching the two sample sizes rather than a cylindrical form, (the default for the soda can crusher).

Here are the liquid helium temperature results

Notice that the current goes up with the smaller sample size.  It would seem there should be a sweet spot between size and current.

Here are the results of the magnetic field calculation along the surface of the sphere as the coordinate on the z axis, (here shown on the x axis of the graph), increases.  The small sample size will quench comfortably, while the big sample will not be completely immersed in a quenching field.  The next step is to try the simulation again with a 5000 volt charge on the capacitors instead of the 3000 volts that is being used now.

Here’s the math for determining the cylindrical radius required by the magnetic field function for the z coordinate with an axis along a sphere that is slightly smaller than the sample size.

Background

Hirsch's theory of hole superconductivity proposes a new BCS-compatible model of Cooper pair formation when superconducting materials phase transition from their normal to their superconducting state[1].  One of the experimentally verifiable predictions of his theory is that when a superconductor rapidly transitions, (quenches), back to its normal state, it will emit x-rays, (colloquially referred to here as H-rays because it's Hirsch's theory).

A superconductor can be rapidly transitioned back to its normal state by placing it in a strong magnetic field.  My experiment will look for H-rays emitted by both a Pb and a YBCO superconductor when it is quenched by a strong magnetic field.

This series of articles chronicles both the experimental lab work and the theory work that’s going into completing the experiment.

The lab book entries in this series detail the preparation and execution of this experiment… mostly.  I also have a few theory projects involving special relativity and quantum field theory.  Occasionally, they appear in these pages.

Call for Input

If you have any ideas, questions, or comments, they're very welcome!

References

1.  Hirsch, J. E., “Pair production and ionizing radiation from superconductors”, http://arxiv.org/abs/cond-mat/0508529