Imagine living thousands of years ago in ancient Sumeria as a mathematician. Your medium for storing infomration is cuneiform on clay tablets. As you work, you stamp each equation into wet clay by making wedge shaped marks using the blunt end of a reed to make a finished document that looks like this (picture 1)[1]
When your instructor tells you to investigate the properties of a table of let's say, a hundred numbers or so, you might sigh in resignation, and plan on having results by sometime next week.
With the advent of paper and pencil, things become much easier. There's still lots of work to be done, but the recording of the information so that it can be viewed and worked with is, comparatively speaking, a piece of cake.
Finally, though, the computer comes along and getting a table of 100 numbers is more like playing. With +The SageMathCloud the 100 number task suggested in the +Mathematical Association of America video below can be done easily by anyone with a web browser. Watch the video[2] and then read on for an example of just that.
The problem is to figure out the maximum slope, a, for a line described by y = 2 + m*x where 1/2 < m < a. The game is that the line cannot intersect with any lattice points. These are points where the x and y coordinates both have integer values. The first minute or so of the video has a great illustration of this. So, we don't want to hit any of the blue lattice points shown in picture 2 as we crank up the slope of the line to the value m < a.
Dr. Tanton suggested that we take a look at the value of the line with slope m = 1/2 and how far it was from each of the lattice points directly above it out to the x coordinate of 100. Here's the graph of the m = 1/2 line as well as the lattice points that we need to avoid as we crank the slope up from 1/2. (picture 2)
and, here's the sage code if you'd like to play with it
Now, instead of figuring out the slope that would hit each successive 'bad' lattice point, we can have Sage do it for us, and dump it out as a list of slopes at each point. Cick the blue button below for the table of slopes necessary to just hit each lattice point. In other words, by staying less than each successive slope, we can just miss that lattice point.
We see that the slope which will hit the 99th lattice point we're trying to miss is 50/99. So, in the problem as asked, the maximum the slope, a can be is a < 50/99.
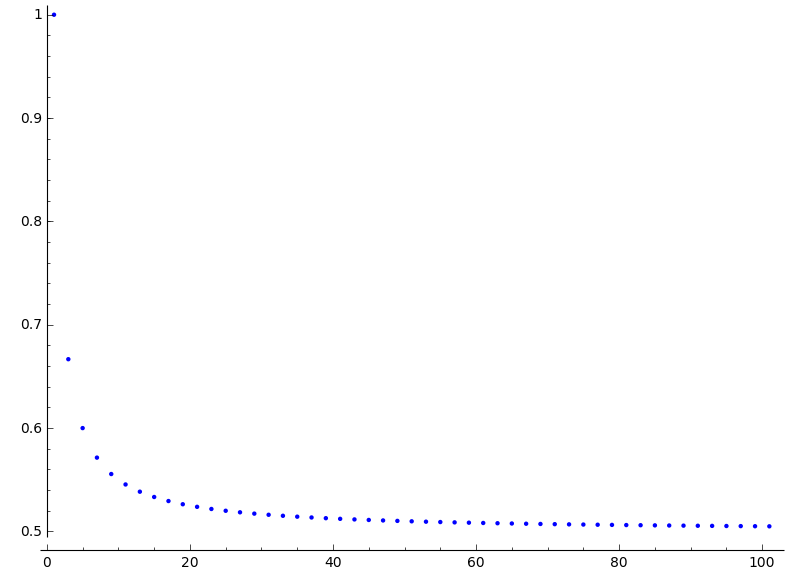
Another snazzy thing we can look at is how the maximum slope progressed as we went from lattice point to lattice point out towards 99. Here's the graph: (picture 3)
Here's the Sage code used to generate it. Remember you can modify the sage code in any of these cells and hit the blue button again to find out what effect your modifications had.
References:
1. http://books.google.com/books?id=i-juAAAAMAAJ&pg=PR3#v=onepage&q&f=false
2. Video
http://youtu.be/j2J6NEGTMsY
When your instructor tells you to investigate the properties of a table of let's say, a hundred numbers or so, you might sigh in resignation, and plan on having results by sometime next week.
With the advent of paper and pencil, things become much easier. There's still lots of work to be done, but the recording of the information so that it can be viewed and worked with is, comparatively speaking, a piece of cake.
Finally, though, the computer comes along and getting a table of 100 numbers is more like playing. With +The SageMathCloud the 100 number task suggested in the +Mathematical Association of America video below can be done easily by anyone with a web browser. Watch the video[2] and then read on for an example of just that.
The problem is to figure out the maximum slope, a, for a line described by y = 2 + m*x where 1/2 < m < a. The game is that the line cannot intersect with any lattice points. These are points where the x and y coordinates both have integer values. The first minute or so of the video has a great illustration of this. So, we don't want to hit any of the blue lattice points shown in picture 2 as we crank up the slope of the line to the value m < a.
Dr. Tanton suggested that we take a look at the value of the line with slope m = 1/2 and how far it was from each of the lattice points directly above it out to the x coordinate of 100. Here's the graph of the m = 1/2 line as well as the lattice points that we need to avoid as we crank the slope up from 1/2. (picture 2)
and, here's the sage code if you'd like to play with it
Now, instead of figuring out the slope that would hit each successive 'bad' lattice point, we can have Sage do it for us, and dump it out as a list of slopes at each point. Cick the blue button below for the table of slopes necessary to just hit each lattice point. In other words, by staying less than each successive slope, we can just miss that lattice point.
We see that the slope which will hit the 99th lattice point we're trying to miss is 50/99. So, in the problem as asked, the maximum the slope, a can be is a < 50/99.
Another snazzy thing we can look at is how the maximum slope progressed as we went from lattice point to lattice point out towards 99. Here's the graph: (picture 3)
Here's the Sage code used to generate it. Remember you can modify the sage code in any of these cells and hit the blue button again to find out what effect your modifications had.
References:
1. http://books.google.com/books?id=i-juAAAAMAAJ&pg=PR3#v=onepage&q&f=false
2. Video
http://youtu.be/j2J6NEGTMsY


Comments
Post a Comment
Please leave your comments on this topic: