Just a few brief notes on circular and hyperbolic trigonometry today. First, if there's anyone who'd like to offer, any clarifications, expansions, or other cool and interesting facts, please, you're more than welcome! As usual, this is stuff that I learned in high school that didn't become blindingly clear and meaningful until it cropped up in grad school physics. First, the equations for the circle and the hyperbola (picture 1)
Notice that they differ only by a single negative sign. Now, for their graphs, (picture 2).
Each of these figures can also be expressed in parametric form as follows, (this is where the trigonometric and hyperbolic trig functions come in). (picture 3)
Now for the notes and other thoughts.
Angular Arc Length and Angular Area
Until just a few weeks ago, I had always wondered why the inverse trig functions were called arcsine, and arccosine. The answer makes perfect sense, it just hadn't occurred to me. The arc prefix indicates that the function returns the arc length around the unit circle for the angle whose value of sine, (for example), is the input to the function. A numeric example shows it pretty well. Suppose we take a right angle, equal to pi/2 in radians, and calculate it's sine. The value returned will be 1, and obviously if I plug that into arcsine, I'll get back the angle, pi/2, but.... On the unit circle, the angle is also equal to the arc length around the circle, (circumference from the x axis to the angle), so while it's true that arcsine returns the angle for the value of sine it's given, it's also returning the arc length around the circle for that angle, hence the name.
Hyperbolic trig functions share a similar property, their inverse function return the area between the x axis and an angle line drawn out to the hyperbola from the origin. In the figure shown from Wikipedia[1], the red area is equal to half the angle returned by arcsinh for the hyperbolic angle measured by the line from the origin to the hyperbola.
Here's where we get into the stuff I don't know enough about yet, but which makes for interesting extra reading.
Geometric Algebra
David Hestenes has been writing about geometric algebra and how it can be applied to better understand physics since the mid '60s [2]. His articles are very, very interesting, and I highly recommend them and wish I had more time to read through them. In each of his articles on geometric algebra, the fact that the square root of -1, i, can be interpreted geometrically as an area or volume always comes up. I don't know if one has anything to do with the other, (and I don't have time to check right now which is part of why I'm recording these speculative notes here), but hyperbolic sine and cosine can be represented in the following form using complex numbers
So, we have sine and cosine sprinkled with imaginary numbers and we wind up with something that traces out area rather than arc length.
The Special Relativity Angle
You might have noticed that the infinitesimal line length mentioned in the gamma derivation post a few days back[3] looked kind of like the Pythagorean theorem, but with a few minus signs that didn't quite fit.
These minus signs essentially put calculations in special relativity into a hyperbolic, or Minkowski, geometry[4], and the end result is the use of hyperbolic trigonometric functions throughout. More about this soon.
References:
1. Wikipedia on hyperbolic trigonometric funcitons
http://en.wikipedia.org/wiki/Hyperbolic_sine
2. Hestenes' Oersted medal lecture
http://dx.doi.org/10.1119%2F1.1522700
Hestenes D. (2003). Oersted Medal Lecture 2002: Reforming the mathematical language of physics, American Journal of Physics, 71 (2) 104. DOI: 10.1119/1.1522700
open access
http://c2.com/cgi/wiki?HestenesOerstedMedalLecture
3. Rindler's derivation of gamma
http://copaseticflow.blogspot.com/2013/06/rindlers-just-flat-out-pretty.html
4. On Minkowski geometry
http://www.dynamicgeometry.com/documents/advancedSketchGallery/minkowski/Minkowski_Overview.pdf
Notice that they differ only by a single negative sign. Now, for their graphs, (picture 2).
Each of these figures can also be expressed in parametric form as follows, (this is where the trigonometric and hyperbolic trig functions come in). (picture 3)
Now for the notes and other thoughts.
Angular Arc Length and Angular Area
Until just a few weeks ago, I had always wondered why the inverse trig functions were called arcsine, and arccosine. The answer makes perfect sense, it just hadn't occurred to me. The arc prefix indicates that the function returns the arc length around the unit circle for the angle whose value of sine, (for example), is the input to the function. A numeric example shows it pretty well. Suppose we take a right angle, equal to pi/2 in radians, and calculate it's sine. The value returned will be 1, and obviously if I plug that into arcsine, I'll get back the angle, pi/2, but.... On the unit circle, the angle is also equal to the arc length around the circle, (circumference from the x axis to the angle), so while it's true that arcsine returns the angle for the value of sine it's given, it's also returning the arc length around the circle for that angle, hence the name.
Hyperbolic trig functions share a similar property, their inverse function return the area between the x axis and an angle line drawn out to the hyperbola from the origin. In the figure shown from Wikipedia[1], the red area is equal to half the angle returned by arcsinh for the hyperbolic angle measured by the line from the origin to the hyperbola.
Here's where we get into the stuff I don't know enough about yet, but which makes for interesting extra reading.
Geometric Algebra
David Hestenes has been writing about geometric algebra and how it can be applied to better understand physics since the mid '60s [2]. His articles are very, very interesting, and I highly recommend them and wish I had more time to read through them. In each of his articles on geometric algebra, the fact that the square root of -1, i, can be interpreted geometrically as an area or volume always comes up. I don't know if one has anything to do with the other, (and I don't have time to check right now which is part of why I'm recording these speculative notes here), but hyperbolic sine and cosine can be represented in the following form using complex numbers
So, we have sine and cosine sprinkled with imaginary numbers and we wind up with something that traces out area rather than arc length.
The Special Relativity Angle
You might have noticed that the infinitesimal line length mentioned in the gamma derivation post a few days back[3] looked kind of like the Pythagorean theorem, but with a few minus signs that didn't quite fit.
These minus signs essentially put calculations in special relativity into a hyperbolic, or Minkowski, geometry[4], and the end result is the use of hyperbolic trigonometric functions throughout. More about this soon.
References:
1. Wikipedia on hyperbolic trigonometric funcitons
http://en.wikipedia.org/wiki/Hyperbolic_sine
2. Hestenes' Oersted medal lecture
http://dx.doi.org/10.1119%2F1.1522700
Hestenes D. (2003). Oersted Medal Lecture 2002: Reforming the mathematical language of physics, American Journal of Physics, 71 (2) 104. DOI: 10.1119/1.1522700
open access
http://c2.com/cgi/wiki?HestenesOerstedMedalLecture
3. Rindler's derivation of gamma
http://copaseticflow.blogspot.com/2013/06/rindlers-just-flat-out-pretty.html
4. On Minkowski geometry
http://www.dynamicgeometry.com/documents/advancedSketchGallery/minkowski/Minkowski_Overview.pdf
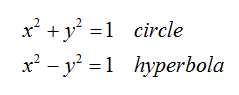





nice
ReplyDelete