Rindler demonstrates[2] the best way ever to derive the relativistic Lorentz contraction/time dilation factor, gamma, (of twin paradox fame), from four velocity! I've been working through Rindler's paper on hyperbolic motion as a result of constant acceleration[1] lately.
Starting from the constancy of the speed of light, Einstein's theory of special relativity posited, and Minkowski refined the idea that the universe is actually four dimensional with space and time sitting on an equal footing. Starting from here, we can write an expression for the distance squared along an infinitesimal line element in four dimensions, (think Pythagorean theorem)...
Brian Greene popularized the idea of four velocity[3] in one of his books and although it isn't mentioned as much as some of the other aspects of special rel, it's a simple idea. Everything is moving at the speed of light. Something might have more of it's velocity pointed into either the space dimensions, or the time dimension, but at the end of the day, its four dimensional speed is equal to the speed of light, c. So, let's write down the infinitesimal distance along a four dimensional line divided by an infinitesimal amount of time as a velocity
and we're done!
References:
1. http://dx.doi.org/10.1103%2FPhysRev.119.2082
Rindler W. (1960). Hyperbolic Motion in Curved Space Time, Physical Review, 119 (6) 2082-2089. DOI: 10.1103/PhysRev.119.2082
2. Special Relativity by Wolfgang Rindler
http://books.google.com/books?id=8kqBAAAAIAAJ
3. On four velocity
Starting from the constancy of the speed of light, Einstein's theory of special relativity posited, and Minkowski refined the idea that the universe is actually four dimensional with space and time sitting on an equal footing. Starting from here, we can write an expression for the distance squared along an infinitesimal line element in four dimensions, (think Pythagorean theorem)...
Brian Greene popularized the idea of four velocity[3] in one of his books and although it isn't mentioned as much as some of the other aspects of special rel, it's a simple idea. Everything is moving at the speed of light. Something might have more of it's velocity pointed into either the space dimensions, or the time dimension, but at the end of the day, its four dimensional speed is equal to the speed of light, c. So, let's write down the infinitesimal distance along a four dimensional line divided by an infinitesimal amount of time as a velocity
which can be rearranged to give
From here on out, it's all Rindler. Factor the increment of time out of the above expression
At this point, the velocity, (distance over time), squared is sitting in the second term, so we can write
Leaving us with
Which can be rearranged once again to give
Which is the formula for time dilation, (the time in the moving frame is equal to gamma times the time in the rest frame), so
References:
1. http://dx.doi.org/10.1103%2FPhysRev.119.2082
Rindler W. (1960). Hyperbolic Motion in Curved Space Time, Physical Review, 119 (6) 2082-2089. DOI: 10.1103/PhysRev.119.2082
2. Special Relativity by Wolfgang Rindler
http://books.google.com/books?id=8kqBAAAAIAAJ
3. On four velocity

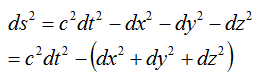

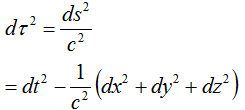





Comments
Post a Comment
Please leave your comments on this topic: