The Importance of the Law of Cosines

Just a quick note on the more generic and far lest cited sibling of the Pythagorean theorem, the law of cosines. If you're like me, you were taught this formula sometime between the eighth and the eleventh grades and promptly forgot it after your exam. It's a formula that relates the length of one side of a triangle (any side), to its opposite angle and the lengths of the other two sides. The formula and its associated diagram, (courtesy of Wikipedia), are shown below:

If you keep it in mind, you'll start to see it show up all over the place, honest! For example it turned up in today's electromagnetism homework. We were tasked on determining the electrostatic potential at any point in a plane due to a ring of charge. Some of us put a significant amount of effort into determining a general formula for the distance from a point in the plane to any point on the circle. An industrious eight grader however, could have rattled the formula off by heart!

References:
http://en.wikipedia.org/wiki/Law_of_cosines

Picture of the Day:

From 1/25/13

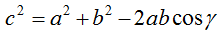
Comments

Cool Math Tricks: Deriving the Divergence, (Del or Nabla) into New (Cylindrical) Coordinate Systems

Now available as a Kindle ebook for 99 cents ! Get a spiffy ebook, and fund more physics The following is a pretty lengthy procedure, but converting the divergence, (nabla, del) operator between coordinate systems comes up pretty often. While there are tables for converting between common coordinate systems , there seem to be fewer explanations of the procedure for deriving the conversion, so here goes! What do we actually want? To convert the Cartesian nabla to the nabla for another coordinate system, say… cylindrical coordinates. What we’ll need: 1. The Cartesian Nabla: 2. A set of equations relating the Cartesian coordinates to cylindrical coordinates: 3. A set of equations relating the Cartesian basis vectors to the basis vectors of the new coordinate system: How to do it: Use the chain rule for differentiation to convert the derivatives with respect to the Cartesian variables to derivatives with respect to the cylindrical variables. The chain ...

The Alcubierre Warp Drive Tophat Function and Open Science with Sage

I transferred yesterday's Mathematica file with the Alcubierre warp drive[2] line element and space curvature calculations to the +Sage Mathematical Software System today, (the files been added to the public repository [3]). If you haven't used Sage before, it's a Python based software package that's similar in functionality to Mathematica. Oh, and it' free. I also worked a little more on understanding the theory, but frankly, I made far more progress with the software than the theory. What follows will be a little more of the Alcubierre theory, plus, a cool Sage interactive demo of one of the Alcubierre functions[1], as well as a bit about my first experience with using Sage. Theory The theory is fun, but it's moving slowly. Here's the chalk board from this morning's discussion Alcubierre setup the derivation using something called the 3+1 formalism which means we consider space to be flat, (in this case), slices that are labelled ...

The Valentine's Day Magnetic Monopole

There's an assymetry to the form of the two Maxwell's equations shown in picture 1. While the divergence of the electric field is proportional to the electric charge density at a given point, the divergence of the magnetic field is equal to zero. This is typically explained in the following way. While we know that electrons, the fundamental electric charge carriers exist, evidence seems to indicate that magnetic monopoles, the particles that would carry magnetic 'charge', either don't exist, or, the energies required to create them are so high that they are exceedingly rare. That doesn't stop us from looking for them though! Keeping with the theme of Fairbank[1] and his academic progeny over the semester break, today's post is about the discovery of a magnetic monopole candidate event by one of the Fairbank's graduate students, Blas Cabrera[2]. Cabrera was utilizing a loop type of magnetic monopole detector. Its operation is in...

Copasetic Flow

Search This Blog