Qualitative Superconductor Hysteresis Monitoring: Lab Book 2014_12

Qualitative Superconductor Hysteresis Monitoring: Lab Book 2014_12_30

Lab Book 2014_12_30

Today I worked on getting a qualitative susceptometer up and running. By qualitative I mean that we won't be attempting to analyze the returned data to accurately determine any characteristics of the superconducting materials that are to be studied, only the state of the materials, and the existence, or not of a hysteresis curve for the material.

The why of it all

I’m experimenting with a quick and dirty susceptometer that can be used with the hray experiment to determine when we’ve quenched the superconductor. Today’s work is using a ferromagnetic core, not a superconductor. The responses are similar and I don’t have to worry about cooling a superconductor.

Experimental Setup

Something old and something new

I’m pressing a General Radio 1311-A audio oscillator and a Tektronix TDS 210 into service together.

The general radio signal generator is being used to drive the coil surrounding the iron core. The oscilloscope is measuring both the signal from the General Radio source and the pickup coil on the iron core as shown below

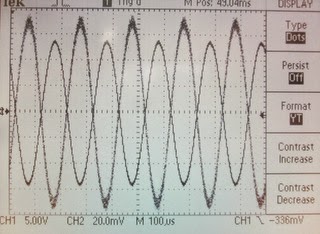
Voltage vs. time vs. frequency

In the following waveforms, the driving voltage is on channel 1 and the response voltage from the pickup coil is shown on channel two. Channel one is a cleaner signal than channel two. There’s a 180 degree phase difference between the signal just as you’d expect from Lenz’s law and the output on the pickup coil increases with frequency as you’d expect from Faraday’s law.

400 Hz	500 Hz	1000 Hz	2000 Hz	5000 Hz	10000 Hz

X-Y data vs. frequency

The expected hysteresis loop began to appear once the frequency of the generator was brought sufficiently high. The following data table illustrates this.

400 Hz
500 Hz
1000 Hz
2000 Hz
5000 Hz
10000 Hz

The final data point at 10,000 Hz is shown below with bandwidth limiting on the scope enabled to cut down on the signal noise:

What we’re seeing

As the frequency of the oscillator is increased, the loop is opening up because the ferromagnetic response of the core can’t track quickly enough with the driving current. Consequently there’s a phase difference between the two signals and this appears in the x-y display mode as a gradually opening loop.

It should be noted that the signal isn’t large enough to cause the iron core to saturate. If it was, we’d see horizontal flat extensions at either corner of the loop. A power amplifier may be added to the arrangement tomorrow to cause saturation.

Here’s a set of hysteresis curves that depend on frequency[1]. Notice that the enclosed loop becomes wider as the frequency increases, just as in the data shown above.

How Ferromagnets and Superconductors are Alike, (well, one way anyway)

I mentioned that ferromagnets behaved in a similar manner to superconductors when subjected to a magnetic field. It’s because their hysteresis curves don’t look too much different. Here’s a hysteresis curve[2] measured for superconducting Pb. The square is the theoretically ideal response. The curved lines are the actual response of the superconductor.

References:

1. Jiles, J.C., “Frequency dependence of hysteresis curves in conducting magnetic materials

”, Journal of Applied Physics 76, 5849 (1994) http://dx.doi.org.lib-ezproxy.tamu.edu:2048/10.1063/1.358399

2. Rjabinin, Shubnikow, “Dependence of Magnetic Induction on the Magnetic Field in Supraconducting Lead”, Nature, 134, (1934), 286-287

Cool Math Tricks: Deriving the Divergence, (Del or Nabla) into New (Cylindrical) Coordinate Systems

Now available as a Kindle ebook for 99 cents ! Get a spiffy ebook, and fund more physics The following is a pretty lengthy procedure, but converting the divergence, (nabla, del) operator between coordinate systems comes up pretty often. While there are tables for converting between common coordinate systems , there seem to be fewer explanations of the procedure for deriving the conversion, so here goes! What do we actually want? To convert the Cartesian nabla to the nabla for another coordinate system, say… cylindrical coordinates. What we’ll need: 1. The Cartesian Nabla: 2. A set of equations relating the Cartesian coordinates to cylindrical coordinates: 3. A set of equations relating the Cartesian basis vectors to the basis vectors of the new coordinate system: How to do it: Use the chain rule for differentiation to convert the derivatives with respect to the Cartesian variables to derivatives with respect to the cylindrical variables. The chain ...

The Alcubierre Warp Drive Tophat Function and Open Science with Sage

I transferred yesterday's Mathematica file with the Alcubierre warp drive[2] line element and space curvature calculations to the +Sage Mathematical Software System today, (the files been added to the public repository [3]). If you haven't used Sage before, it's a Python based software package that's similar in functionality to Mathematica. Oh, and it' free. I also worked a little more on understanding the theory, but frankly, I made far more progress with the software than the theory. What follows will be a little more of the Alcubierre theory, plus, a cool Sage interactive demo of one of the Alcubierre functions[1], as well as a bit about my first experience with using Sage. Theory The theory is fun, but it's moving slowly. Here's the chalk board from this morning's discussion Alcubierre setup the derivation using something called the 3+1 formalism which means we consider space to be flat, (in this case), slices that are labelled ...

The Valentine's Day Magnetic Monopole

There's an assymetry to the form of the two Maxwell's equations shown in picture 1. While the divergence of the electric field is proportional to the electric charge density at a given point, the divergence of the magnetic field is equal to zero. This is typically explained in the following way. While we know that electrons, the fundamental electric charge carriers exist, evidence seems to indicate that magnetic monopoles, the particles that would carry magnetic 'charge', either don't exist, or, the energies required to create them are so high that they are exceedingly rare. That doesn't stop us from looking for them though! Keeping with the theme of Fairbank[1] and his academic progeny over the semester break, today's post is about the discovery of a magnetic monopole candidate event by one of the Fairbank's graduate students, Blas Cabrera[2]. Cabrera was utilizing a loop type of magnetic monopole detector. Its operation is in...

Copasetic Flow

Search This Blog