Watching the Alfred Leitner film on superconductors brought up quite a few things I didn't fully understand about the energy gap of superconductors.
I frequently run into a problem when reading physics books and articles and especially when watching physics lectures. If the writer/presenter doesn't outline in broad details where they're headed, a few deleterious, (for me), effects ensue. First, I'm likely to lose interest altogether. Second, since I don't know what the point of the discussion is I usually fail to grasp the few key facts that are embedded within. This has happened each of the several times I've set out to learn or be taught the details of the energy gap in superconductors. The same thing almost happened again as I watched Leitner's lecture on the subject, (video excerpt below). Consequently, I thought it might be handy to provide a bit of an outline of the key points in the explanation if, like me, you'd rather know where you're headed before you get there. By the way, if you'd like a very nice article on energy gaps in general, check out this post[1] form +Jonah Miller.
OK,here we go. First off...
What the experiment and the superconductor energy gap is not about
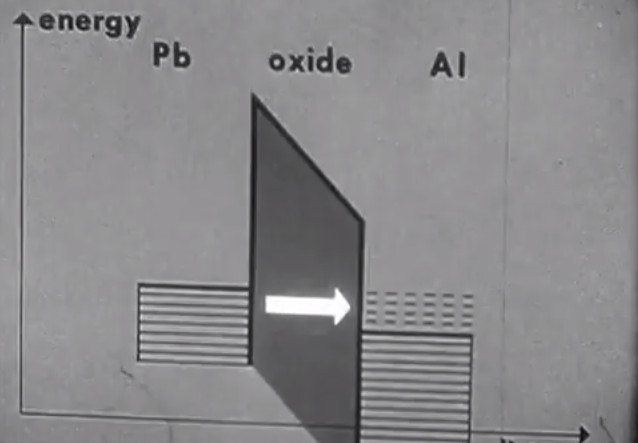
The tunneling experiment that finds the superconducting energy gap has nothing to do with the superconductor per se. All metals, even in their normal state exhibit tunneling behavior. I finally put this together after watching the clip below twice and gawking when I saw the first example of tunneling where Dr. Leitner wrote T > 7.2 K, (picture 1). In other words, the experiment was done above the superconducting transition temperature of both lead and aluminum, the two metals used in the tunneling junction.
In summary, tunneling is a quantum mechanical effect, but it does not require a superconductor. Metals in their normal states will do quite nicely, thank you.
As a related ancillary point, the energy gap experiment has nothing to do with Josephson junctions. These tunneling junctions are very specific to superconductors and function because of very specific superconductor behavior. Even though the junction configurations look the same, and the names sound the same, the tunneling experiment to determine the superconducting energy gap has nothing to do with Josephson junctions.
And now:
What we're actually watching for
Electrons tunnel from one metal to another through an insulator at near zero temperatures because the number of occupied energy states in the two different metals is different.
As Dr. Leitner points out, almost all metals will exhibit tunneling behavior. The two metals involved, lead and aluminum, have different Fermi energy levels, (the maximum energy level that electrons are allowed to occupy before they become conducting). To ensure that all the electrons in the metals are at or below the Fermi energy level, the metal does need to have a temperature near absolute zero. Hence, the experiment does have to be done at very low temperatures. Because of quantum mechanical tunneling, the metal with more occupied levels will see the metal, (even through an insulator), with fewer occupied levels and the electrons in the first, more occupied, metal will tunnel to the second, less occupied metal, (picture 2).
This process continues until the occupied levels equalize. The end result is that the metal, (lead in our case), with fewer levels effectively has its potential raised, (picture 3).
Now, when a voltage is applied between the lead and aluminum contacts, electrons will tunnel from the lead to unoccupied excited energy states in the aluminum, (picture 4).
And Here's Where Superconductors Do Something Different
Here's the punch line. Because of the energy gap in a superconductor, tunneling will actually stop when the lead sample enters its superconducting state. There are energy states that are forbidden to electrons in the superconducting lead. These disallowed states are known as the energy gap of the superconductor. In the picture below they are the levels between the bold black line and the dotted line on the lead side of the insulator, (picture 5).
In this case, electrons won't flow from the aluminum side to the lead side to equalize the energy levels. Electrons also won't flow from the lead side to the aluminum side, even when a voltage is applied, until enough voltage is added to the lead side to move the bold line above the level of the bold demarcated energy level on the aluminum side, basically moving the superconducting lead energy gap up and out of the way, (picture 6).
At this point, tunneling occurs again just as it did for the lead sample in the normal state. Be sure to watch the video below for all the details, the above is just a very widely brushstroked sketch.
Here's one last note of historical interest. Ivar Giaever[2], a graduate student working at General Electric in 1960 is credited with doing the first experiment that showed the superconduting energy gap discussed above. This experiment resulted in him sharing the 1973 Nobel prize with Leo Esaki and Brian Josephson. It was the work of Giaever that inspired the later work of Josephson whom the Josephson junction is named after.
References:
1. Jonah Miller on energy gaps
http://www.thephysicsmill.com/2013/02/03/im-with-the-valence-band-band-structure-and-the-science-of-conduction/
2. Ivar Giaever
https://en.wikipedia.org/wiki/Ivar_Giaever
3. On the battle between Bardeen and Josephson over tunelling
http://www.physics.umd.edu/courses/Phys798I/anlage/AnlageFall12/Josephson%20Physics%20Today%205153075.pdf
4. permalink to this post
http://copaseticflow.blogspot.com/2014/05/the-superconducting-energy-gap.html
I frequently run into a problem when reading physics books and articles and especially when watching physics lectures. If the writer/presenter doesn't outline in broad details where they're headed, a few deleterious, (for me), effects ensue. First, I'm likely to lose interest altogether. Second, since I don't know what the point of the discussion is I usually fail to grasp the few key facts that are embedded within. This has happened each of the several times I've set out to learn or be taught the details of the energy gap in superconductors. The same thing almost happened again as I watched Leitner's lecture on the subject, (video excerpt below). Consequently, I thought it might be handy to provide a bit of an outline of the key points in the explanation if, like me, you'd rather know where you're headed before you get there. By the way, if you'd like a very nice article on energy gaps in general, check out this post[1] form +Jonah Miller.
OK,here we go. First off...
What the experiment and the superconductor energy gap is not about
The tunneling experiment that finds the superconducting energy gap has nothing to do with the superconductor per se. All metals, even in their normal state exhibit tunneling behavior. I finally put this together after watching the clip below twice and gawking when I saw the first example of tunneling where Dr. Leitner wrote T > 7.2 K, (picture 1). In other words, the experiment was done above the superconducting transition temperature of both lead and aluminum, the two metals used in the tunneling junction.
In summary, tunneling is a quantum mechanical effect, but it does not require a superconductor. Metals in their normal states will do quite nicely, thank you.
As a related ancillary point, the energy gap experiment has nothing to do with Josephson junctions. These tunneling junctions are very specific to superconductors and function because of very specific superconductor behavior. Even though the junction configurations look the same, and the names sound the same, the tunneling experiment to determine the superconducting energy gap has nothing to do with Josephson junctions.
And now:
What we're actually watching for
Electrons tunnel from one metal to another through an insulator at near zero temperatures because the number of occupied energy states in the two different metals is different.
As Dr. Leitner points out, almost all metals will exhibit tunneling behavior. The two metals involved, lead and aluminum, have different Fermi energy levels, (the maximum energy level that electrons are allowed to occupy before they become conducting). To ensure that all the electrons in the metals are at or below the Fermi energy level, the metal does need to have a temperature near absolute zero. Hence, the experiment does have to be done at very low temperatures. Because of quantum mechanical tunneling, the metal with more occupied levels will see the metal, (even through an insulator), with fewer occupied levels and the electrons in the first, more occupied, metal will tunnel to the second, less occupied metal, (picture 2).
This process continues until the occupied levels equalize. The end result is that the metal, (lead in our case), with fewer levels effectively has its potential raised, (picture 3).
Now, when a voltage is applied between the lead and aluminum contacts, electrons will tunnel from the lead to unoccupied excited energy states in the aluminum, (picture 4).
And Here's Where Superconductors Do Something Different
Here's the punch line. Because of the energy gap in a superconductor, tunneling will actually stop when the lead sample enters its superconducting state. There are energy states that are forbidden to electrons in the superconducting lead. These disallowed states are known as the energy gap of the superconductor. In the picture below they are the levels between the bold black line and the dotted line on the lead side of the insulator, (picture 5).
In this case, electrons won't flow from the aluminum side to the lead side to equalize the energy levels. Electrons also won't flow from the lead side to the aluminum side, even when a voltage is applied, until enough voltage is added to the lead side to move the bold line above the level of the bold demarcated energy level on the aluminum side, basically moving the superconducting lead energy gap up and out of the way, (picture 6).
At this point, tunneling occurs again just as it did for the lead sample in the normal state. Be sure to watch the video below for all the details, the above is just a very widely brushstroked sketch.
Here's one last note of historical interest. Ivar Giaever[2], a graduate student working at General Electric in 1960 is credited with doing the first experiment that showed the superconduting energy gap discussed above. This experiment resulted in him sharing the 1973 Nobel prize with Leo Esaki and Brian Josephson. It was the work of Giaever that inspired the later work of Josephson whom the Josephson junction is named after.
References:
1. Jonah Miller on energy gaps
http://www.thephysicsmill.com/2013/02/03/im-with-the-valence-band-band-structure-and-the-science-of-conduction/
2. Ivar Giaever
https://en.wikipedia.org/wiki/Ivar_Giaever
3. On the battle between Bardeen and Josephson over tunelling
http://www.physics.umd.edu/courses/Phys798I/anlage/AnlageFall12/Josephson%20Physics%20Today%205153075.pdf
4. permalink to this post
http://copaseticflow.blogspot.com/2014/05/the-superconducting-energy-gap.html





Comments
Post a Comment
Please leave your comments on this topic: