A Different Way to Memorize the Taylor Series and a Cry For Mathematical Help
As an undergrad, and throughout my graduate career until now, I've always had a hard time remembering how to apply a Taylor series. I knew there were coefficients in front of powers of x and that those coefficients somehow involved derivatives of the function I was trying to aproximate with the Taylor series, but that was aobut it. Even when I looked up the formula, there was still always some initial confusion. I'd arrive at an equation that looked like the following
followed by a little bit of text blithely informing that if I'd only take the nth derivative of both sides of the equation, and evaluate the derivative at x = b, then of course I'd see that the coefficient a sub n could be written as
As an undergrad, and throughout my graduate career until now, I've always had a hard time remembering how to apply a Taylor series. I knew there were coefficients in front of powers of x and that those coefficients somehow involved derivatives of the function I was trying to aproximate with the Taylor series, but that was aobut it. Even when I looked up the formula, there was still always some initial confusion. I'd arrive at an equation that looked like the following
followed by a little bit of text blithely informing that if I'd only take the nth derivative of both sides of the equation, and evaluate the derivative at x = b, then of course I'd see that the coefficient a sub n could be written as
This inevitably led to having to remember that the first n-1 terms in the sum would become zero after they were differentiated n times, and that the terms of n+1 and above would become zero when x was equal to b so that only the term containing a sub n was left. Perhaps I'm a bit slow, but that was my process every single time.
Looking at the formulas last night for the umpteenth time, it occurred to me that the first two terms in the Taylor series are how we approximate functions when we only want to add a small change in x. We get the value for the function at x equals b, then approximate the function as a straight line and multiply the slope of that line times a small change in x to get the approximate value of the function at the location b plus our small change in x
In other words, we as the question, how does our function change for a small change in x, (what's it's slope with respect to x?), and then multiply that slope by our small change in x to get the associated small change in the function.
Now, look at a Taylor series with three terms:
The second term is the slope with respect to x I just mentioned. If we write the second derivative in a different notation, we have
which, when I squint at it in just the right light looks for all the world like the amount my function will change for a small change in x squared. An then with a second look, I see that the derivative is in fact multiplied by x squared. It's slightly more visible if we take b equal to zero, and rewrite the series as:
This looks kind of great! A Taylor series is just a series of corrections that ask what's the slope of my function with respect to a power of x and then multiplies that slope by the particular power of x. That's far easier for me to remember, but there's still one issue left. What about the annoying factors of one over n factorial out in front of each term?
And, that brings me to my second mathematical sin for the day, or more politely worded, my second opportunity to be mathematically clarified. I'm calling it the inverse chain rule. The chain rule provides a way to take the derivatives of composite functions like
by first taking the derivative of the outer function, (cosine in this case), with respect to its argument, (x squared in this case), then determining how the argument changes with respect to x and finally determining the entire change with respect to x by multiplying the two changes together. So, using the chain rule, I can ask the question: how does my function of x squared change with respect to x?
A Little Formal Math Help Please?
In my above reasoning, I've asked the inverse of the chain rule question. I'm asking, (for the third term), how my function of x varies with respect to x squared. The terms of n factorial are just one over the nth derivative of the power of x I'm interested in
Since I've asked the inverse of the chain rule question question, I'm guessing that instead of multiplying [the derivative of the my function with respect to x to the n] by [the derivative of x to the n with respect to x] that multiplying by the inverse of [the derivative of x to the n with respect to x]. I know this is correct because it gives the correct terms for a Taylor series, but I don't know how to say it formally or explain it completely. Would anyone like to clarify... please?
Summary of the Method
So, at the end of the day, the way I will now always remember the Taylor series is as a set of patches in powers of x to an approximtaion. I multiply each power of x by the slope of the function with respect to that power of x. To take care of the inverse chain rule, if the power is n, I then divide by the nth derivative of the nth power of x, (also known as n factorial).
Picture of the Day:
| From 1/27/13 |



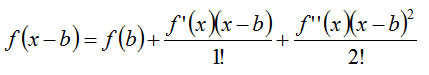




Comments
Post a Comment
Please leave your comments on this topic: