One of the first tasks in this project has been to determine what the Podkletnov apparatus should do when it is operated and what physical mechanisms account for each aspect of the operation. In Dr. Podkletnov's papers, he points out that the disc is rotated with the use of solenoids that are placed around the superconducting disc in a number of configurations as shown below. I'll compare these configurations to other existing superconductor motor research in a future entry.
From EE Podkletnov, arxiv, (1997), http://arxiv.org/abs/cond-mat/9701074
The above diagram shows the two phase coils that are wrapped through the disc. The magnetic field inside these solenoids will be parallel to the surface of the disc. The dashed circles indicate the levitation solenoids that lie below the disc.
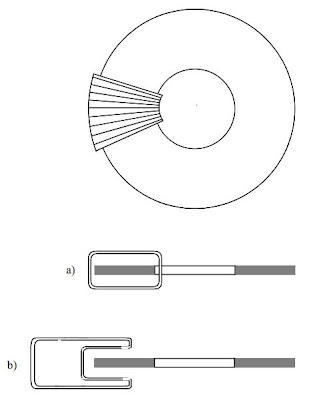
The next diagram is a detail of one of the through wrapped solenoids as well as a second solenoid configuration in which the solenoid windings are bent out of the way of the disc. To be clear, in a) the solenoid is wrapped around the disc from the outside, along the surface and through the hole in the center. In b), apparently, the solenoid is wrapped so that its axis is parallel to the axis of rotation of the disc. The middle of the solenoid is then pushed towards its center to make room for the disc to pass between the un-pushed windings.
From EE Podkletnov, arxiv, (1997), http://arxiv.org/abs/cond-mat/9701074
The next two configuration utilize what appears to be a ferromagnetic yoke with either one, (a), or two, (b), solenoids wrapped around it. The magnetic field in this arrangement will be perpendicular to the surface of the superconducting disc.
From EE Podkletnov, arxiv, (1997), http://arxiv.org/abs/cond-mat/9701074
The following diagram seems to detail the positioning of the yokes with respect to the superconducting disc, although, there is not text in Dr. Podkletnov's paper explaining the diagram:
From EE Podkletnov, arxiv, (1997), http://arxiv.org/abs/cond-mat/9701074
Finally, notice in this last diagram that there appears to be a pivot supporting the disc. This is also not mentioned in the paper. The paper indicates that the disc is supported by levitating magnetic fields from solenoids below the disc.
From EE Podkletnov, arxiv, (1997), http://arxiv.org/abs/cond-mat/9701074
From EE Podkletnov, arxiv, (1997), http://arxiv.org/abs/cond-mat/9701074
The above diagram shows the two phase coils that are wrapped through the disc. The magnetic field inside these solenoids will be parallel to the surface of the disc. The dashed circles indicate the levitation solenoids that lie below the disc.
The next diagram is a detail of one of the through wrapped solenoids as well as a second solenoid configuration in which the solenoid windings are bent out of the way of the disc. To be clear, in a) the solenoid is wrapped around the disc from the outside, along the surface and through the hole in the center. In b), apparently, the solenoid is wrapped so that its axis is parallel to the axis of rotation of the disc. The middle of the solenoid is then pushed towards its center to make room for the disc to pass between the un-pushed windings.
From EE Podkletnov, arxiv, (1997), http://arxiv.org/abs/cond-mat/9701074
The next two configuration utilize what appears to be a ferromagnetic yoke with either one, (a), or two, (b), solenoids wrapped around it. The magnetic field in this arrangement will be perpendicular to the surface of the superconducting disc.
From EE Podkletnov, arxiv, (1997), http://arxiv.org/abs/cond-mat/9701074
The following diagram seems to detail the positioning of the yokes with respect to the superconducting disc, although, there is not text in Dr. Podkletnov's paper explaining the diagram:
From EE Podkletnov, arxiv, (1997), http://arxiv.org/abs/cond-mat/9701074
Finally, notice in this last diagram that there appears to be a pivot supporting the disc. This is also not mentioned in the paper. The paper indicates that the disc is supported by levitating magnetic fields from solenoids below the disc.
From EE Podkletnov, arxiv, (1997), http://arxiv.org/abs/cond-mat/9701074




Comments
Post a Comment
Please leave your comments on this topic: