My review of the material I mentioned yesterday[1] paid off pretty quickly. Dr. Hirsch is quick to point out that one of the key differences between his 'hole theory of superconductivity'[4] and the more typical explanation of Cooper pair formation is that his theory predicts
kinetic energy lowering after two holes in an energy band pair
as opposed to the usual
potential energy lowering after two electrons pair.
While reading Hirsch's articles, I didn't remember ever coming across kinetic energy lowering pairing before. It turned out that I had read about it in Dr. Likharev's notes, (see section 2.6, 'Coupled Quantum Wells'), but without an immediate application for the information, I promptly forgot it.
Here are the basics
1. Crystalline materials, (like superconductors, or semiconductors), in which electrons reside can be very roughly modeled as repeated delta function wells, (picture 1)[2] where the delta functions represent the potentials electrons encounter at each crystal lattice site. (For an excellent, basic introduction to crystals, see Holden and Morrison's "Crystals and Crystal Growing".[3] This book fascinated me when I was in elementary school and it still does.)
2. If we look at a pair of wells represented by three of these delta functions, we can create a rough model of how two electrons, (or holes), in neighboring wells might interact with each other. The important condition of this model, for our discussion, is that the quantum mechanical wave function for each electron must equal zero at the wall of the well, (represented by the delta function).
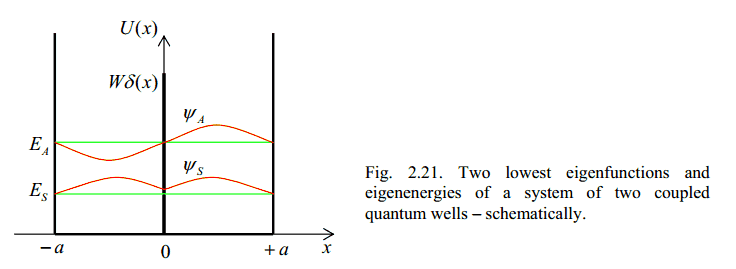
This condition leads to two possible lowest energy wave functions shown in picture 2[2]. These are labelled S for symmetric and A for anti-symmetric.
3. The energy of a particle in quantum mechanics is proportional to it's frequency. Frequency is inversely proportional to wavelength. So, the anti-symmetric wave function above which has a longer overall wavelength, (spanning two wells instead of one), has a lower kinetic energy than the symmetric one.
4. Dr. Likharev points out that the anti-symmetric wave function is rough example of a covalent chemical bond between atoms. Each of a pair of electrons have spread their wave function to encompass two atoms and occupy the same orbit around the two atoms. The two electrons can occupy the same orbit as long as they have opposite spins. Dr. Likharev goes on to point out that covalent bonds are stronger than ionic bonds and that they are formed by kinetic energy lowering. (seep picture 3)
This is the same kinteic energy lowering that Hirsch employs in his derivations, albeit in a different application, the pairing of holes at the onset of superconductivity.
Interesting Historical Sidelight
Using the energy stored in the covalent bonds of N2 was once studied as a rocket fuel. The idea was to break the bonds, store the resulting monatomic nitrogen, and then utilize the kinetic energy expended when the gas explosively recombined to propel a rocket.
References:
1. Yesterday's post
http://copaseticflow.blogspot.com/2014/06/brillouin-zones-band-gaps-bloch.html
2. Dr. Likharev's notes
http://goo.gl/SE5QmF
3. Crystals and Crystal Growing
http://books.google.com/books?id=Sco5b7N4Pb8C&lpg=PP1&dq=crystal&pg=PP1#v=onepage&q=crystal&f=false
4. Hirsch, J. E., “Pair production and ionizing radiation from superconductors”,
http://arxiv.org/abs/cond-mat/0508529
Hirsch's theory of hole superconductivity proposes a new BCS-compatible model of Cooper pair formation, when superconducting materials phase transition from their normal to their superconducting state. One of the experimentally verifiable predictions of his theory is that when a superconductor rapidly transitions, (quenches), back to its normal state, it will emit x-rays, (colloquially referred to here as H-rays because it's Hirsch's theory).
A superconductor can be rapidly transitioned back to its normal state by placing it in a strong magnetic field. The experiment being performed proposes to look for H-rays emitted by a Pb superconductor when it is quenched by a strong magnetic field.
This series of articles chronicles both the experimental lab work and the theory work that’s going into completing the experiment.
kinetic energy lowering after two holes in an energy band pair
as opposed to the usual
potential energy lowering after two electrons pair.
While reading Hirsch's articles, I didn't remember ever coming across kinetic energy lowering pairing before. It turned out that I had read about it in Dr. Likharev's notes, (see section 2.6, 'Coupled Quantum Wells'), but without an immediate application for the information, I promptly forgot it.
Here are the basics
1. Crystalline materials, (like superconductors, or semiconductors), in which electrons reside can be very roughly modeled as repeated delta function wells, (picture 1)[2] where the delta functions represent the potentials electrons encounter at each crystal lattice site. (For an excellent, basic introduction to crystals, see Holden and Morrison's "Crystals and Crystal Growing".[3] This book fascinated me when I was in elementary school and it still does.)
2. If we look at a pair of wells represented by three of these delta functions, we can create a rough model of how two electrons, (or holes), in neighboring wells might interact with each other. The important condition of this model, for our discussion, is that the quantum mechanical wave function for each electron must equal zero at the wall of the well, (represented by the delta function).
This condition leads to two possible lowest energy wave functions shown in picture 2[2]. These are labelled S for symmetric and A for anti-symmetric.
3. The energy of a particle in quantum mechanics is proportional to it's frequency. Frequency is inversely proportional to wavelength. So, the anti-symmetric wave function above which has a longer overall wavelength, (spanning two wells instead of one), has a lower kinetic energy than the symmetric one.
4. Dr. Likharev points out that the anti-symmetric wave function is rough example of a covalent chemical bond between atoms. Each of a pair of electrons have spread their wave function to encompass two atoms and occupy the same orbit around the two atoms. The two electrons can occupy the same orbit as long as they have opposite spins. Dr. Likharev goes on to point out that covalent bonds are stronger than ionic bonds and that they are formed by kinetic energy lowering. (seep picture 3)
This is the same kinteic energy lowering that Hirsch employs in his derivations, albeit in a different application, the pairing of holes at the onset of superconductivity.
Interesting Historical Sidelight
Using the energy stored in the covalent bonds of N2 was once studied as a rocket fuel. The idea was to break the bonds, store the resulting monatomic nitrogen, and then utilize the kinetic energy expended when the gas explosively recombined to propel a rocket.
References:
1. Yesterday's post
http://copaseticflow.blogspot.com/2014/06/brillouin-zones-band-gaps-bloch.html
2. Dr. Likharev's notes
http://goo.gl/SE5QmF
3. Crystals and Crystal Growing
http://books.google.com/books?id=Sco5b7N4Pb8C&lpg=PP1&dq=crystal&pg=PP1#v=onepage&q=crystal&f=false
4. Hirsch, J. E., “Pair production and ionizing radiation from superconductors”,
http://arxiv.org/abs/cond-mat/0508529
Hirsch's theory of hole superconductivity proposes a new BCS-compatible model of Cooper pair formation, when superconducting materials phase transition from their normal to their superconducting state. One of the experimentally verifiable predictions of his theory is that when a superconductor rapidly transitions, (quenches), back to its normal state, it will emit x-rays, (colloquially referred to here as H-rays because it's Hirsch's theory).
A superconductor can be rapidly transitioned back to its normal state by placing it in a strong magnetic field. The experiment being performed proposes to look for H-rays emitted by a Pb superconductor when it is quenched by a strong magnetic field.
This series of articles chronicles both the experimental lab work and the theory work that’s going into completing the experiment.


Comments
Post a Comment
Please leave your comments on this topic: