Lab Book 2014_05_14 YBCO levitation, Glass Dewar Mechanics, and Relativistic Projectile Trajectories
Lab Book 2014_05_14 Hamilton Carter
This lab notebook entry documents testing a YBCO superconductor for magnetic levitation, troubleshooting a jammed glass Dewar stopcock, and exploring mathematical parallels between relativistic projectile trajectories and classical drag models.
Summary:
Tested the larger of the two YBCO superconductors by trying out three different levitation demonstrations. Ran into a hitch when preparing to vacuum test the glass Dewar. The glass stopcock valve to the vacuum jacket is stuck shut! Unbeknownst to me, you can replace glass valves! Did a bit of theory work looking at hyperbolic trajectories of relativistic particles and how they compare to the trajectories of projectiles with air resistance.Lab Work: YBCO Rough Characterization
The YBCO superconductor was levitation tested. Although it’s not a quantitative measure, it seems to be levitating magnets as well as it ever did. I ran a series of three demonstrations showing the different types of field cooling/levitation. In the first experiment, the superconductor was cooled without the magnet present. Since the sample was very well constructed using a crystal melt method, there aren’t a whole lot of imperfections for magnetic flux to pentetrate into. The magnet levitates as it would over a type I superconductor that rejects all flux. In other words, it won’t levitate stably and falls off the opposing field created by the superconductor to one side of the cup or the other.
In the second demo, the superconductor was cooled with the
magnet already in place, suspended by a thread a small distance above the
sample. The magnetic flux lines
penetrate the superconductor before it enters its superconducting state and are
trapped there. When the superconductor
has been cooled and the suspension string loosened, the magnet levitates. The superconductor also remembers where the
flux lines were located after the magnet is removed. When the magnet is dropped back down onto the
superconductor, its landing is cushioned and it is directed back to its
previous levitated location.
In the third case, the magnet is placed directly on the
superconductor. Once again, the lines of
magnetic field are frozen in. This time
however, do to the proximity of the magnet to the superconductor, the
superconductor won’t let the magnet be pulled apart from it. Effectively, the superconductor is behaving
like a second magnet.
Lab Work: Leak Detector Hookup and Jammed Dewar Stopcock
The leak detector was hooked up to the rubber hose that will evacuate the vacuum jacket on the glass Dewar.
We immediately ran into an issue, however. The glass stopcock that seals the vacuum
jacket was stuck shut.
At the advice of the glass shop we tried to heat the stopcock
with a heat gun to loosen it. The effort
was unsuccessful. I didn’t realize it,
but glass stopcocks can actually be replaced.
The glass blower removed our stopcock and will replace it on Friday.
Theory Work: Relativistic Projectiles and their Classically Dragged Counterparts
In addition to having everything you ever wanted to know about classical trajectories of projectiles under the influence of a uniform gravitational field, McAllen includes a section on projectiles with air resistance. In particular he includes the following figure and formula.
The right hand side of equation 2 is the innards of an anti-Gudermannian
and only needs to be wrapped in a logarithm to be the anti-Gudermannian itself. Interestingly, the left hand side of the
equation is the logarithmic derivative of the particles velocity with respect
to its angle with the ground as it moves along its trajectory. The diagram is very
reminiscent of the range of a relativistic projectile vs. the angle of launch. Here’s a graph of the relativistic range as
defined by MacColl:
You might notice that this formula also contains an
anti-Gudermannian, however in this guise it’s written as the arctanh of a sine
function. Notice that as the factor u in
the formula above goes to infinity, it will simply cancel out of the
expression.
Here’s the interesting part of the problem. The u factor
determines how close the projectile is to the speed of light and in fact does
approach infinity as the projectile approaches the speed of light. When the particle hits of the speed of light two
things happen. First, the factor of u
cancels out and the range formula is a cosine function times an
anti-Gudermannian. Second, the the optimal
launch angle for maximum range is equal to 56.46 degrees. This is the same angle that will maximize the
path length of the trajectory in the classical problem.
We’ve known for a while that the special relativistic
effects are all tangential in this problem.
It’s very interesting, yet not unexpected, that the air resistance,
(which is also a tangential effect), problem has a few similarities.
Theory Work: Rotating
Frames and Airplanes
Looking into Frenet Serret equations and Fermi-Walker transport. Leinaas and Korsbaken are using a FS frame and not necessarily a FW frame. This is mentioned at one point. Letaw is more careful about that. Svaiter and Letaw are more concerned about detectors that rotate, (spin).
Looking into Frenet Serret equations and Fermi-Walker transport. Leinaas and Korsbaken are using a FS frame and not necessarily a FW frame. This is mentioned at one point. Letaw is more careful about that. Svaiter and Letaw are more concerned about detectors that rotate, (spin).




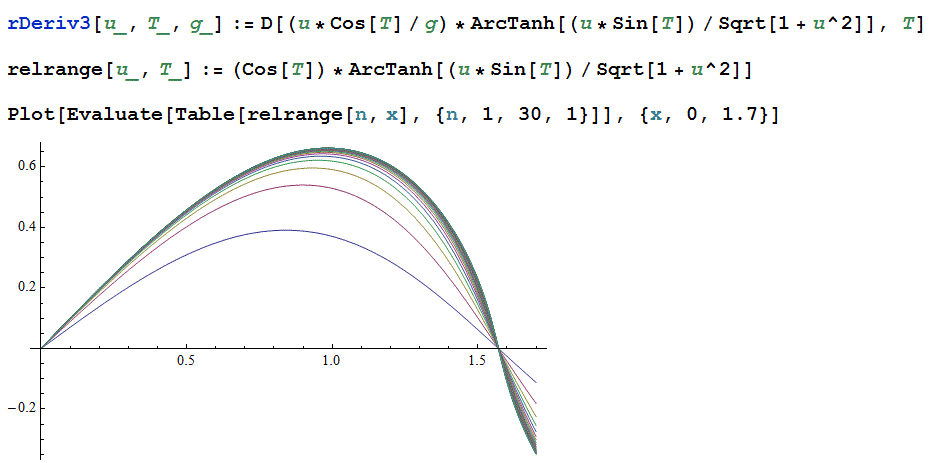
Comments
Post a Comment
Please leave your comments on this topic: