Skip to main content

Bra Ket Notation

Just a few notes here about shiny things that caught my eye regarding bra and ket notation in the quantum mechanics II lecture last night.

Inner Products
Inner products are the Hilbert space, quantum mechanical, state vector equivalent of the dot product for more standard vectors like position or velocity.  The unit basis ket , at least in our class, is written as

where j is the index of the component.  Associating back to Cartesian coordiantes, 1 would denote x, 2 would denote y, and 3 would denote z.  The ket vector is the same symbol in a ket and when the two are applied to each other we get the inner product

.

In other words, the inner product only produces contributions from like basis vectors, just like the dot product.

So here's the cool bit, the following all accomplish about the same thing, they find a number proportional to the magnitude of the component of one vector, lying along another vector whether those  vectors are what we most typically call vectors, or what we call bras and kets, or what we call wavefunctions:




The Projection Operator
Applying the following notation, (the projection operator), had continued to confuse me until last week.


To pull out the portion of a bra vector that points along the basis vector u sub j, the above can be applied as follows:


Applying the projection operator always seemed a bit daunting to me until I saw the entire operation written in several steps utilizing the associative property and the fact that bras and kets commute with scalars as

.

Cool note:
The projection operator is an example of an outer product.  An outer product of two vectors produces a square matrix.  The trace of the matrix is equal to the dot, (or inner), product of the two vectors.

Picture of the Day:
From 1/21/13
Labels:

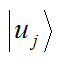
Comments

Post a Comment

Please leave your comments on this topic:

Popular posts from this blog

The Valentine's Day Magnetic Monopole

There's an assymetry to the form of the two Maxwell's equations shown in picture 1.  While the divergence of the electric field is proportional to the electric charge density at a given point, the divergence of the magnetic field is equal to zero.  This is typically explained in the following way.  While we know that electrons, the fundamental electric charge carriers exist, evidence seems to indicate that magnetic monopoles, the particles that would carry magnetic 'charge', either don't exist, or, the energies required to create them are so high that they are exceedingly rare.  That doesn't stop us from looking for them though! Keeping with the theme of Fairbank[1] and his academic progeny over the semester break, today's post is about the discovery of a magnetic monopole candidate event by one of the Fairbank's graduate students, Blas Cabrera[2].  Cabrera was utilizing a loop type of magnetic monopole detector.  Its operation is in concept very sim
1 comment
Read more

Cool Math Tricks: Deriving the Divergence, (Del or Nabla) into New (Cylindrical) Coordinate Systems

Now available as a Kindle ebook for 99 cents ! Get a spiffy ebook, and fund more physics The following is a pretty lengthy procedure, but converting the divergence, (nabla, del) operator between coordinate systems comes up pretty often. While there are tables for converting between common coordinate systems , there seem to be fewer explanations of the procedure for deriving the conversion, so here goes! What do we actually want? To convert the Cartesian nabla to the nabla for another coordinate system, say… cylindrical coordinates. What we’ll need: 1. The Cartesian Nabla: 2. A set of equations relating the Cartesian coordinates to cylindrical coordinates: 3. A set of equations relating the Cartesian basis vectors to the basis vectors of the new coordinate system: How to do it: Use the chain rule for differentiation to convert the derivatives with respect to the Cartesian variables to derivatives with respect to the cylindrical variables. The chain
11 comments
Read more

More Cowbell! Record Production using Google Forms and Charts

First, the what : This article shows how to embed a new Google Form into any web page. To demonstrate ths, a chart and form that allow blog readers to control the recording levels of each instrument in Blue Oyster Cult's "(Don't Fear) The Reaper" is used. HTML code from the Google version of the form included on this page is shown and the parts that need to be modified are highlighted. Next, the why : Google recently released an e-mail form feature that allows users of Google Documents to create an e-mail a form that automatically places each user's input into an associated spreadsheet. As it turns out, with a little bit of work, the forms that are created by Google Docs can be embedded into any web page. Now, The Goods: Click on the instrument you want turned up, click the submit button and then refresh the page. Through the magic of Google Forms as soon as you click on submit and refresh this web page, the data chart will update immediately. Turn up the:
Post a Comment
Read more