In electromagnetism, we came across the following formula describing a potential on a plane (picture 1)
We were to estimate why the potential on the plane didn't go to zero everywhere when the z in the pre-integral numerator seemed to indicate that it did. Very roughly speaking, the points within the denominator blow up to infinity and conspire to cancel the numerators 0. There's a more elegant and rigorous way, (courtesy of my professor), to show that everything is all right though. Here's a sketch of the technique.
What we want to do is show that when the denominator goes to infinity while the numerator is zero, things cancel nicely and we still get a finite answer. When the denominator goes to infinity, the following conditions apply (picture 3)
We want to approximate the potential at locations near where these conditions arise. It's easier to do this using cylindrical coordinates, and we make the following substitutions (picture 4)
For a nice explanation on where the dx-prime times dy-prime element of area substitution came from and for a nice way to think about spherical divergences, see this post[1]. Having made that substitution, the integral above can now be written as (picture 5)
Making the additional substitution w = rho squared we get (picture 6)
This integral can be fairly easily evaluated to get (picture 7)
Where we've taken the integral in the limit where the radius squared goes to zero. Notice that the first term very nicely cancels the z over 2 pi in the pre-integral factor in the original formula above!
References:
1. http://copaseticflow.blogspot.com/2012/09/an-intuitive-way-to-spherical-gradient.html
In our problem, we were given a plane that looked like the following. The potential inside the small square is V and the potential everywhere else is on the plane is zero (picture 2)
We were to estimate why the potential on the plane didn't go to zero everywhere when the z in the pre-integral numerator seemed to indicate that it did. Very roughly speaking, the points within the denominator blow up to infinity and conspire to cancel the numerators 0. There's a more elegant and rigorous way, (courtesy of my professor), to show that everything is all right though. Here's a sketch of the technique.
What we want to do is show that when the denominator goes to infinity while the numerator is zero, things cancel nicely and we still get a finite answer. When the denominator goes to infinity, the following conditions apply (picture 3)
We want to approximate the potential at locations near where these conditions arise. It's easier to do this using cylindrical coordinates, and we make the following substitutions (picture 4)
For a nice explanation on where the dx-prime times dy-prime element of area substitution came from and for a nice way to think about spherical divergences, see this post[1]. Having made that substitution, the integral above can now be written as (picture 5)
Making the additional substitution w = rho squared we get (picture 6)
This integral can be fairly easily evaluated to get (picture 7)
Where we've taken the integral in the limit where the radius squared goes to zero. Notice that the first term very nicely cancels the z over 2 pi in the pre-integral factor in the original formula above!
References:
1. http://copaseticflow.blogspot.com/2012/09/an-intuitive-way-to-spherical-gradient.html


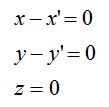




Comments
Post a Comment
Please leave your comments on this topic: